Внеклассное мероприятие по математике, 5 класс

Сценарий внеклассного мероприятия по математике «Математическое кафе» для школьников 5 класса

Оформление. На стенах зала - 3 плаката:

1) Только сегодня, только у нас

Работает единственное в мире

Математическое кафе!

 

2) Подходите, подбегайте

И билетик покупайте!

Только денег не давайте –

На вопросы отвечайте!

 

3) Милости просим,

Милые гости,

В кафе заходите

И место займите!

Ход мероприятия

«Посетителям» кафе предлагаются входные билеты; они отвечают на вопросы и за это получают билеты. Все рассаживаются согласно своему знаку зодиака. Создается б команд (по 2 знака зодиака). Столы различаются цветом букетов, стоящих на столе (розовый, синий, красный, зелёный, жёлтый и оранжевый). На столах стоят самовары, сладости к чаю.

Ведущий. Здравствуйте, дорогие посетители кафе! Наше кафе не простое - математическое.

Чтобы чашки с чаем получить,

Надо будет кое-что решить.

Это кое-что лежит в конверте,

Разверните и проверьте.

На столах лежат конверты, в них - задания.

I. Конкурс «Разминка».

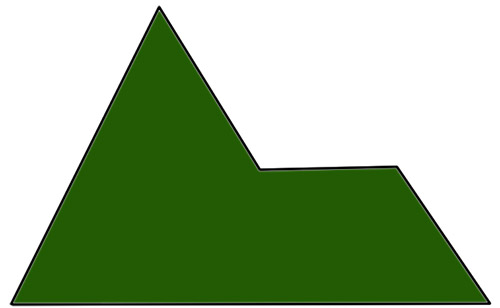
1) Разрежьте данную фигуру на 2 равные части.

2) Разрежьте фигуру на 4 равные части, схожие с оригиналом.

3) На картине Дюрера зашифрован год её написания. Отгадайте и запишите этот год.

(Везде - 34.)

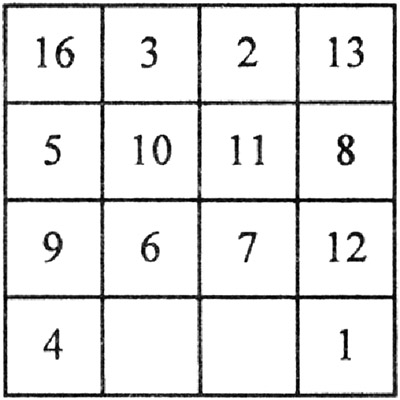
Ответ: 1514 год.

Участникам сообщается, что за каждый верный ответ даётся жетончик (красный кружок). На доске 6 листов, на которые прикрепляются эти жетончики. Если команда не отвечает на свой вопрос, то на него может ответить другая команда.

Ведущий. Знаем, вы хотите кушать,

Но извольте нас послушать:

Дефицит мы продаём –

Посложней вопрос даём.

II. Конкурс «Думай, думай...»

Вопрос «зелёному столу»:

«45 коров надо разместить в 9 загонах так, чтобы в каждом загоне их было разное количество». (В первый загон - 1 корову, во второй - 2, ... , в девятый - 9.)

Вопрос «синему столу»:

«Собрали 100 кг грибов. Оказалось, что их влажность - 99 %. Когда грибы подсохли, влажность их снизилась до 98 %. Какова масса этих грибов после подсушивания?» (50 кг.)

Вопрос «красному столу»:

«После семи стирок размер куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшился вдвое. На сколько ещё стирок хватит этого куска мыла?» (На 1 стирку.)

Вопрос «розовому столу»:

«Рыбаки выловили сетью в ставке 80 рыбин, пометили их и снова выпустили в ставок. На второй день они поймали 150 рыбин, среди которых оказалось 5 помеченных. Сколько всего рыбин в ставке?» (2400 рыбин.)

Примечание. Помеченная рыба равномерно распределяется среди остальных.

Вопрос «жёлтому столу»:

«На одной из улиц Туниса продавались попугаи. Профессор Синицын купил клетку и пошёл покупать попугая. Он спросил продавца, сколько стоит попугай, и тот ответил: “11 динаров с клеткой”.

- А сколько стоит один попугай?

- Попугай на 10 динаров дороже клетки.

Сколько стоит попугай?» (10,5 динаров.)

Вопрос «оранжевому столу»:

«Кузнецу принесли 5 обрывков цепи, состоящей из 3, 4, 5, 6 и 7 звеньев, и предложили соединить все обрывки в одну общую цепь. Какое наименьшее число звеньев надо расковать и снова сковать для выполнения такого задания?» (Обрывок из трёх звеньев расковать и соединить ими остальные звенья.)

III. Конкурс «Раздели тортик».

Ведущий. А теперь вы поедите,

Но прежде тортик разделите!

Каждой команде даётся «тортик», который надо разрезать тремя прямыми так, чтобы каждому из семи ребят достался кусочек торта с розочкой.

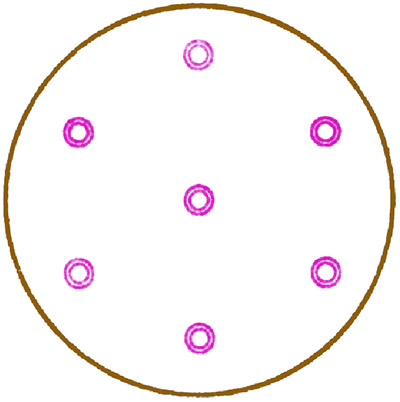
Музыкальная пауза - звучит музыка, предлагается приступить к чаепитию.

IV. Конкурс «Кубики Сома».

Каждой команде предлагается собрать куб из элементов игры «Кубик Сома».

Ведущий. «...Вечно куда-то спешат, ни минуты свободного времени... некогда ни присесть, ни подумать, а если в сплошном потоке их развлечений и покажется небольшой просвет - тут как тут Сома, прекрасная Сома...» — писал известный английский писатель Олдос Хаксли.

Кубики Сома изобрёл англичанин Пит Хейн во время лекции Вернера Гейзенберга по квантовой механике. Пока знаменитый физик говорил о пространстве, разрезанном на кубики, живое воображение Пита Хейна подсказало ему формулировку любопытной геометрической теоремы: «Если взять все неправильные фигуры, которые составлены из трёх или четырёх кубиков, склеенных между собою гранями, то из них можно составить куб большего размера».

«Неправильные фигуры» - это те, на которых есть выступы или впадины. Из трёх кубиков можно построить 1 фигуру, из четырёх - 6. Тут же, на лекции Гейзенберга, Пит Хейн прикинул на листке бумаги, что из 7 элементов, склеенных из 27 кубиков, можно составить куб 3x3x3. Фирмы, занимающиеся производством игрушек, выпустили кубики Хейна в продажу под названием «Кубики Сома». Эта игра популярна в скандинавских странах.

V. Конкурс «Блицтурнир».

Ведущий. А теперь продолжим пир,

Но вначале - блицтурнир.

Участникам задают вопросы, кто первым ответит, тот получает жетончик.

1) Гусь стоит 4 рубля и ещё треть того, что он стоит на самом деле. Сколько стоит гусь? (6 рублей.)

2) Сколько граней у неочиненного граненого карандаша? (6 продольных граней и 2 торцовых, всего 8 граней.)

3) Когда мы смотрим на цифру 2, а говорим: «10»? (Когда смотрим на часы, которые показывают 10 минут какого-либо часа. В это время минутная стрелка стоит на цифре 2.)

4) Шесть ног, две головы, а хвост один. Кто это? (Всадник.)

5) Какой год в XX веке можно перевернуть с ног на голову, и он не изменится? (1961.)

6) Как записать число 100, выразив его четырьмя одинаковыми цифрами, не применяя знаков сложения? (99(9/9) = 100.)

7) Разделите число 18 так, чтобы получилась 1. (18 = 1.)

8) Возле лужицы отряд

Длинноногих лягушат,

Очень стройная колонна:

По пять ровно каждый ряд.

 

По 2, по 3, по 4 –

Как ни ставил командир,

Неизменно оставался

Лишним кто-нибудь один.

 

А сейчас в любой пятёрке

Все довольны, все в восторге!

Ну а сколько лягушат

Не в ряду, а в целом?

 

Свой расчет произведи

С правильным прицелом.

Примечание. Учтите, что в лягушачьей колонне менее 10 рядов.

(25 лягушат.)

9) Числа 100 и 90 разделили на одно и то же число. В первом случае в остатке получили 4, а во втором - 18. На какое число делили? (На 24.)

VI. Конкурс «Танграм».

Татрам - старинная китайская игра. В Китае известна под названием «Чи-чао-тю» (хитроумный узор из семи частей).

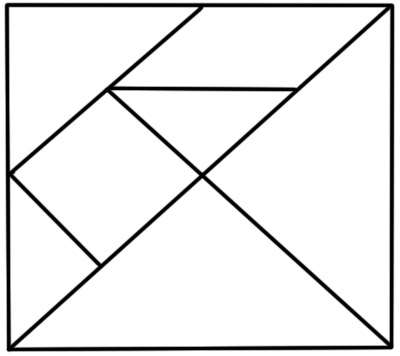
Ребятам выдаются наборы из семи частей и предлагают сначала составить фигурку курочки по готовому рисунку, а затем составить фигурку кошки.

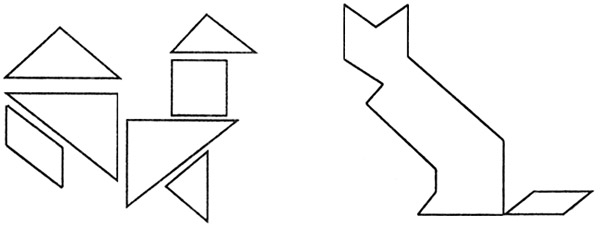
Пока участники собирают фигурку, ведущий рассказывает:

- Эта игра древнее, чем шахматы, хотя и не так хорошо известна. Она возникла в Китае около 4000 лет назад. Она служит любимым развлечением в странах Востока, а с начала XIX в. она получила распространение и на Западе. Рассказывают, что Наполеон, находясь в изгнании на острове Святой Елены, часами занимался составлением картинок из элементов Танграма.

VII. Конкурс «Путешествие в старину».

Ведущий. А теперь «отправимся» в старину.

Небольшой конкурс:

1) Известна пословица: «Мал золотник, да дорог». А сколько это - золотник? (1 золотник = 4,3 грамма.)

2) Что измеряют в баррелях? Сколько это? (Объём нефти, 1 баррель « 159 литров.)

3) Что за единица измерения - лот? (1 лот = 12,9 граммов.)

4) Мера. Что это за единица измерения? (Старая русская мера объёма, мера = 26,24 литра.)

5) А безмен? (Безмен = 1 кг, 1/16 пуда.)

6) Чему равен берковец? (= 10 пудов, 1,64 центнера.)

VIII. Конкурс «Расставь кружки».

Всем раздаются квадраты, разделённые на 16 частей, и по 16 кружочков четырёх цветов, по 4 кружка каждого цвета. Требуется расставить эти кружочки так, чтобы ни по горизонталям, ни по вертикалям, ни по главным диагоналям не встречались кружки одного цвета.

IX. Конкурс «Старинные задачи».

На каждый стол дается 1 задача, и ребята получают время для решения этих задач.

Задача 1. Старинная русская задача.

Некто купил 3/4 аршина сукна и заплатил за них 3 алтына.

Сколько надо заплатить за 100 аршин такого же сукна? (12 рублей.)

Задача 2. Старинная русская задача.

Некто купил 96 гусей. Половину гусей он купил, заплатив по 2 алтына и 7 полушек за каждого гуся. За каждого из остальных гусей он заплатил по 2 алтына без полушки. Сколько стоят гуси? (6 рублей 48 копеек.)

Задача 3. Фазаны и кролики (старинная китайская задача).

В клетке находятся фазаны и кролики. Известно, что всего 35 голов и 94 ноги. Сколько фазанов и сколько кроликов в клетке? (23 фазана и 12 кроликов.)

Задача 4 (из «Курса чистой математики» Войтяховского).

Собака усмотрела в 150 саженях зайца, который пробегает за 2 минуты по 500 саженей, а собака - за 5 минут 1300 саженей. Спрашивается, в какое время собака догонит зайца? (Через 15 с.)

X. Конкурс «Игра “Пентамино”».

«Пента» - по-гречески «пять», это 12 фигурок, составленных разным образом из 5 квадратиков. Каждому участнику выдаётся конверт с 12 частями «Пентамино» и предлагается потренироваться в составлении фигуры петуха по готовому рисунку (сначала петух открыт лишь наполовину, вторая часть закрыта листом бумаги).

Желающие могут попробовать составить другие фигуры по контуру.

XI. Конкурс «Шнурковые головоломки».

Каждому участнику даются шнурковые головоломки. Нужно выполнить задания:

1) Освободить рыбу от пут.

Ответ:

Чтобы снять шнурок в головоломке, нужно протянуть узелок через глаз рыбки, вытянуть и расправить петлю и осторожно протащить ее с лицевой стороны через отверстие в хвосте (под шнурком). Теперь можно пропустить пуговицу через петлю, вытащить петлю назад через хвост, протащить ее обратно через глаз — и все готово. Важно только не перевернуть петлю, иначе рыбка останется в путах.

2) Освободить Луну от пут.

Ответ:

В головоломке, как и в предыдущей, нужно петлю, не переворачивая ее, продеть вслед за шнурком в отверстие А, пропустить через петлю пуговицу (снизу) и вытянуть ее обратно.

XII. Награждение.

Победителям вручаются книжки-малышки, головоломки «Освободи вишенку» и другие призы.

Похожие статьи:

Внеклассное мероприятие по математике, 6 класс